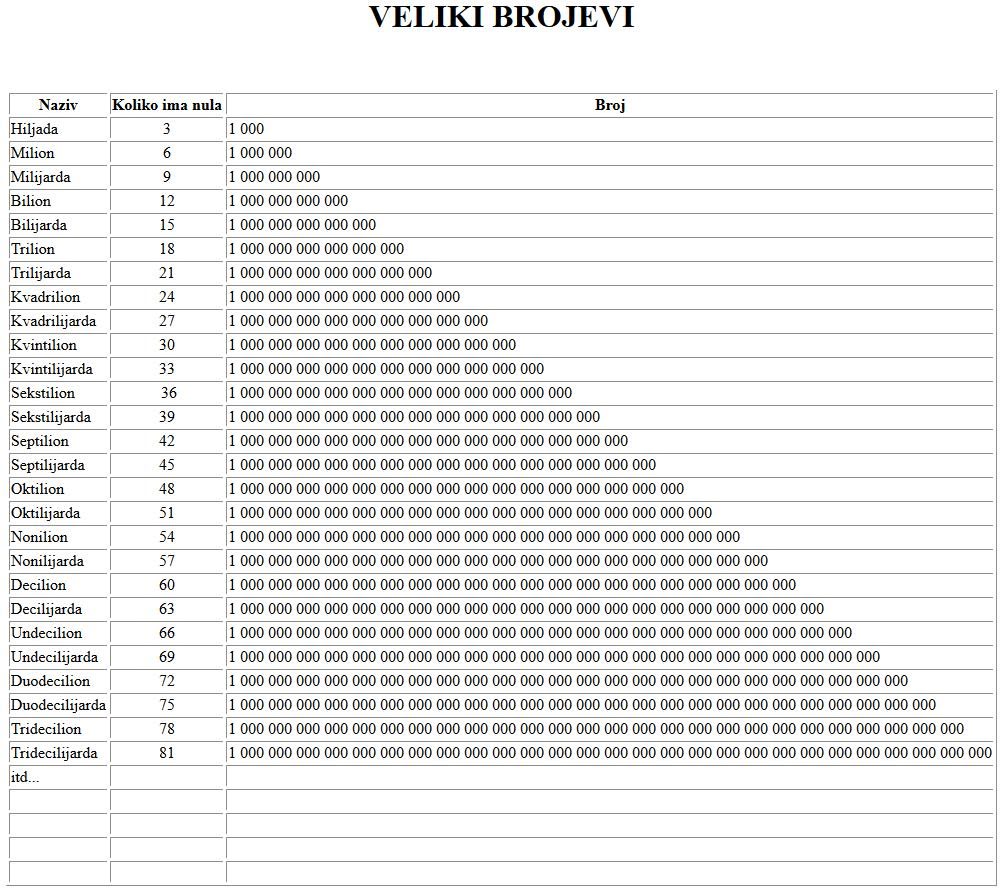
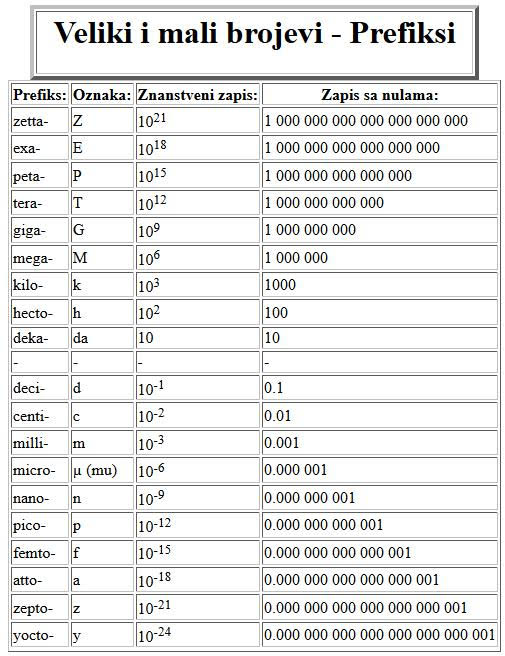
Mnogima je matematika u školi bila najgori i najteži predmet. Ali kad se malo bolje prouči, vjerovali ili ne, može postati vrlo zanimljiva. Matematika voli skladnost, savršenstvo, smislenost,...
Kako biste uvidjeli koliko matematika može biti zanimljiva definirat ću neke osnovne pojmove kao što su savršeni brojevi, brojevi blizanci i sprijateljeni brojevi te ću navesti po nekoliko primjera. Dovoljno je osnovno znanje sabiranja i množenja da se shvati jer su zadaci vrlo jednostavni. Ovo ja zovem "igra brojevima"!
Za početak evo jedan primjer.
Primjer 1:
1 + 2 + 3 + ... + 99 + 100 = 101 * 50 = 5050
Definicija:
SAVRŠENI BROJ je broj kod kojeg je zbir svih njegovih djelitelja (osim njega samog) jednak njemu samom.
Primjer 2:
a) Broj 6
Djelitelji broja 6 koji su različiti od njega samoga su brojevi 1, 2 i 3
Njihov zbir je 1 + 2 + 3 = 6
b) Broj 28
Djelitelji: 1, 2, 4, 7 i 14
Zbir : 1 + 2 + 4 + 7 + 14 = 28
c) Broj 496
Djelitelji: 1, 2, 4, 8, 16, 31, 62, 124 i 248
Zbir: 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Definicija:
PROST BROJ je broj koji je djeljiv samo sa 1 i sa samim sobom.
Definicija:
Prosti brojevi koji se razlikuju za dva zovu se BROJEVI BLIZANCI.
Primjer 3:
Brojevi blizanci su npr. brojevi:
a) 5 i 7
b) 11 i 13
c) 17 i 19
Definicija:
SPRIJATELJENI BROJEVI su parovi brojeva sa svojstvom da je svaki od njih jednak zbiru svih djelitelja (osim njega samoga) svog broja prijatelja.
Primjer 4:
Sprijateljeni brojevi su 220 i 284.
Djelitelji broja 220 različiti od 220: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110
Djelitelji broja 284 različiti od 284: 1, 2, 4, 71, 142
Zbirovi:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
1 + 2 + 4 + 71 + 142 = 220
Jeste li znali ovo? 
Najzanimljiviji primjeri tek slijede!
Primjer 5:
12345679 * 9 = 111111111
12345679 * 18 = 222222222
12345679 * 27 = 333333333
12345679 * 36 = 444444444
12345679 * 45 = 555555555
12345679 * 54 = 666666666
12345679 * 63 = 777777777
12345679 * 72 = 888888888
12345679 * 81 = 999999999
Primjer 6:
0 * 9 + 1 = 1
1 * 9 + 2 = 11
12 * 9 + 3 = 111
123 * 9 + 4 = 1111
1234 * 9 + 5 = 11111
12345 * 9 + 6 = 111111
123456 * 9 + 7 = 1111111
1234567 * 9 + 8 = 11111111
12345678 * 9 + 9 = 111111111
123456789 * 9 + 10 = 1111111111
Primjer 7:
0 * 9 + 8 = 8
9 * 9 + 7 = 88
98 * 9 + 6 = 888
987 * 9 + 5 = 8888
9876 * 9 + 4 = 88888
98765 * 9 + 3 = 888888
987654 * 9 + 2 = 8888888
9876543 * 9 + 1 = 88888888
98765432 * 9 + 0 = 888888888
987654321 * 9 - 1 = 8888888888
Primjer 8:
4^2 = 16
34^2 = 1156
334^2 = 111556
3334^2 = 11115556
33334^2 = 1111155556
333334^2 = 111111555556
3333334^2 = 11111115555556
33333334^2 = 1111111155555556
333333334^2 = 111111111555555556
3333333334^2 = 11111111115555555556
33333333334^2 = 1111111111155555555556
333333333334^2 = 111111111111555555555556
3333333333334^2 = 11111111111115555555555556
i tako dalje...
Primjer 9:
100 = 111 - 11
100 = 99 + 9 : 9
100 = 9 * 9 + 9 + 9 + 9 : 9
100 = 33 * 3 + 3 : 3
100 = 5 * 5 * 5 - 5 * 5
100 = ( 5 + 5 + 5 +5 ) * 5
100 = ( 5 * 5 - 5 ) * 5
100 = ( 5 + 5 ) * ( 5 + 5)
100 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 * 9
100 = 123 - 45 - 67 + 89
100 = 12 : 3 + 4 * 5 - 6 - 7 + 89
Primjer 10:
4 - 4 + 4 - 4 = 0
4 - 4 + ( 4 : 4 ) = 1
( 4 * 4 ) : (4 + 4) = 2
( 4 + 4 + 4 ) : 4 = 3
( 4 - 4 ) * 4 + 4 = 4
( 4 * 4 + 4 ) : 4 = 5
( 4 + 4 ) : 4 + 4 = 6
4 + 4 - ( 4 : 4 ) = 7
4 + 4 + 4 - 4 = 8
4 + 4 + ( 4 : 4 ) = 9
Primjer 11:
1973 = 1111 : 11 + 1111 * ( 1 + 1 ) - ( 11 + 11 + 11 ) * 11 + 11 + 1 + 1
1973 = 2222 - 222 - 22 - 2 * 2 - 2 : 2
1973 = 333 * ( 3 + 3 ) - 33 + 3 * 3 - 3 : 3
1973 = 44 * 44 + 44 - 4 - 4 + 4 : 4
1973 = 55 * 55 - 555 - 555 + 55 + ( 5 + 5 + 5 ) : 5
1973 = 6 * 6 * 6 * 6 + 666 + 66 : 6
1973 = 7777 : 7 + 777 + 77 + 7 + 7 : 7
1973 = ( 8 + 8 + 8 ) * 88 - ( 8 + 8 ) * 8 - 8 - ( 8 + 8 + 8 ) : 8
1973 = 99 * 9 + ( 99 - 9 ) * 9 + 9 * ( 9 + 9 ) + ( 999 - 9 ) : 9
Primjer 12:
9 + 9 = 18 dok je 9 * 9 = 81
24 + 3 = 27 dok je 24 * 3 = 72
47 + 2 = 49 dok je 47 * 2 = 94
263 + 2 = 265 dok je 263 * 2 = 526
497 + 2 = 499 dok je 497 * 2 = 994
Primjer 13:
1 = 1 * 1 / 1
121 = 22 * 22 / ( 1 + 2 + 1 )
12321 = 333 * 333 / ( 1 + 2 + 3 + 2 + 1 )
1234321 = 4444 * 4444 / ( 1 + 2 + 3 + 4 + 3 + 2 + 1 )
123454321 = 55555 * 55555 / ( 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 )
12345654321 = 666666 * 666666 / ( 1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 )
1234567654321 = 7777777 * 7777777 / ( 1 + 2 +3 + 4 + 5 + 6 + 7 + 6 + 5 + 4 + 3 + 2 + 1 )
i tako dalje...
Svako zna TEOREM O PLATI koji kaže da inžinjeri nikada ne mogu zaraditi onoliko novca koliko zarađuju prodavači.
Ovaj teorem može biti objašnjen jednostavnim matematičkim formulama:
Jednačine se baziraju na dva stava:
Stav 1:
Znanje je Moć (Snaga).
Stav 2:
Vrijeme je Novac.
Svaki inžinjer zna da je:
Snaga (Moć) = Rad / Vrijeme
Pa, pošto je:
Znanje = Snaga (Moć)
i
Vrijeme = Novac
Slijedi da je:
Znanje = Rad / Novac
Sada lako dobijamo da je:
Novac = Rad / Znanje
Dakle, kada Znanje teži ka nuli - Novac teži ka beskonačnosti, bez obzira na uložen Rad. To vrijedi čak i kada je uloženi rad izuzetno mali.
I u obrnutom slučaju, kada Znanje teži ka beskonačnosti - dobijeni Novac teži ka nuli, čak i kada je uloženi Rad vrlo veliki.
Zaključak:
Što manje znaš - to više zarađuješ!
Svi oni među vama koji su imali problema u praćenju i shvaćanju teorema i dokaza, sigurno zarađuju puno novca.
"Svako ko misli da je nastavnički posao lagan, neka isproba sljedeću vježbicu.
Uzmi dovoljno vremena u jednom danu i sroči 5 govora, od kojih svaki treba ispuniti 45 minuta, o bilo čemu, u što se ti osobno dobro razumiješ. Pri tome uzmi u obzir da svoju publiku moraš zainteresirati i motivirati na pažnju, slušanje, razumijevanje i usvajanje tog svog govora. Naravno, trebaš smisliti i nekoliko zanimljivih zadataka i aktivnosti koje će tvoju publiku potaknuti na sudjelovanje i interakciju.
Sutra ustani, pristojno se obuci i provozaj se po gradu 30 minuta do sat vremena, vrati se kući, upali televizor i pojačaj ga. Stani pred taj televizor i u 45 minuta ispričaj taj svoj govor i sve što si pripremio/la tako da govoriš glasnije od televizora. S vremenom postepeno pojačavaj televizor (jer učenička pažnja opada i postaju pričljiviji i nezainteresiraniji) te i dalje govori glasnije od televizora. Usput naravno moraš pratiti sve što se na ekranu odvija i program koji gledaš. Kad god netko od ukućana prođe, ti odgovori suvislo na sva njegova pitanja i udovolji svim njegovim zahtjevima.
Naravno, nemoj zaboraviti cijelo to vrijeme biti ugodan i smiren te imati osmjeh na licu kako bi pridonio boljoj atmosferi u prostoriji.
Nakon 45 minuta, uzmi pauzu od 5 minuta, ali tada jako pojačaj televizor, kako bi se dočarao odmor u školi. Po mogućnosti, neka tvoje dijete nekoliko puta protrči pored tebe ili se potuče s bratom ili sestrom. Ti tada smireno i vješto riješi tu situaciju, tako da svi budu zadovoljni.
Zatim vrati televizor na početnu postavku (svejedno glasnije od uobičajene), uzmi svoj drugi pripremljeni govor, zadatke i aktivnosti i ponovi sve u idućih 45 minuta. Opet isti odmor od 5 minuta pa ponovno sve ispočetka, 45 minuta. To radi tako 5 puta zaredom.
Onda pozovi kod sebe komšiju, s kojim imaš neki problem i provedi 45 minuta s njim, smireno i uljudno rješavajući taj problem, objašnjavajući kako i zašto je do njega došlo i predloži kako ga efikasno riješiti.
Kada završiš opet sjedni u auto i vozaj se po gradu 30 minuta do sat vremena. Vrati se kući, malo se odmori (pitam se, hoćeš li upaliti televizor ili imati snage igrati se sa svojom djecom), zatim sjedni i pripremi 5 novih govora za sutra.
Ponovi ovu vježbu 5 dana zaredom pa mi se javi i reci da li još uvijek vjeruješ da je naš posao lagan.
Eto, to ti je profesorska/nastavnička radna sedmica, bez papirologije, dežurstava, pisanja godišnjih, mjesečnih i operativnih planova, razredništva, planiranja i sveg ostalog. Samo radna sedmica".
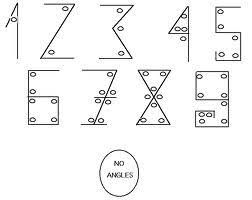
Arapski brojevi јe naziv za sledećih deset cifara: 0 (nula), 1 (jedan), 2 (dva), 3 (tri), 4 (četiri), 5 (pet), 6 (šest), 7 (sedam), 8 (osam), 9 (devet). U dekadnom brojevnom sistemu sa osnovom 10, uz pomoć ovih cifara mogu se predstaviti svi brojevi. Smatra se da njihov zapis ima veze sa brojem uglova koji se formiraju prilikom njihovog pisanja, što se može vidjeti na slici lijevo.
Ukoliko niste do sada znali, klikom na sliku lijevo pogledajte kako se zovu i kako pišu brojevi veći od miliona.
Klikom na sliku lijevo pogledajte na koji način se formiraju veliki i mali brojevi (prefiksi).
Klikom na sliku lijevo pogledajte prezentaciju kako su nastali brojevi.
Klikom na sliku lijevo pogledajte prezentaciju kako su brojevni sistemi.
Klikom na sliku lijevo pogledajte na koji način možemo uspostaviti korelaciju (vezu) između Matematike i Vjeronauke.
Klikom na sliku lijevo pogledajte trikove za lakše računanje.